본 포스팅은 “Do it! 알고리즘 코딩 테스트 자바 편” 의 학습용도입니다.
문제분석하기
- 질의의 개수가 10만이므로, 질의마다 합을 구하면 안되고, 구간 합 배열을 이용해야 한다.
- 구간 합 배열이 1차원에서 2차원으로 확장된 것으로 생각하여 구간 합 배열을 어떻게 구성할지 고민하는 것이 이 문제의 핵심이다.
- 2차원 구간 합 배열은 다음과 같이 정의할 수 있다.
2차원 구간 합 배열 D[X][Y]의 정의
- D[X][Y] = 원본 배열의 (0,0) 부터 (X,Y)까지의 사각형 영역 안에 있는 수의 합
- 1차원 배열 구간 합이 궁금하다면?
백준[11659] - 구간 합 구하기 4
✏️ 문제분석 수의 개수와 합을 구해야 하는 횟수는 최대 10만 구간마다 합을 매번 계산하면 0.5초 안에 모든 구간 합계산을 끝낼 수 없음 💡 구간 합을 매번 계산하면 최악의 경우, 1억 회 이상
muscleking3426.tistory.com
손으로 풀어보기
1️⃣ 2차원 구간 합 배열의 1행 1열 부터 구한다. 구간 합 배열의 1행, 1열은 다음과 같이 구할 수 있다.
i : 행 / j : 열
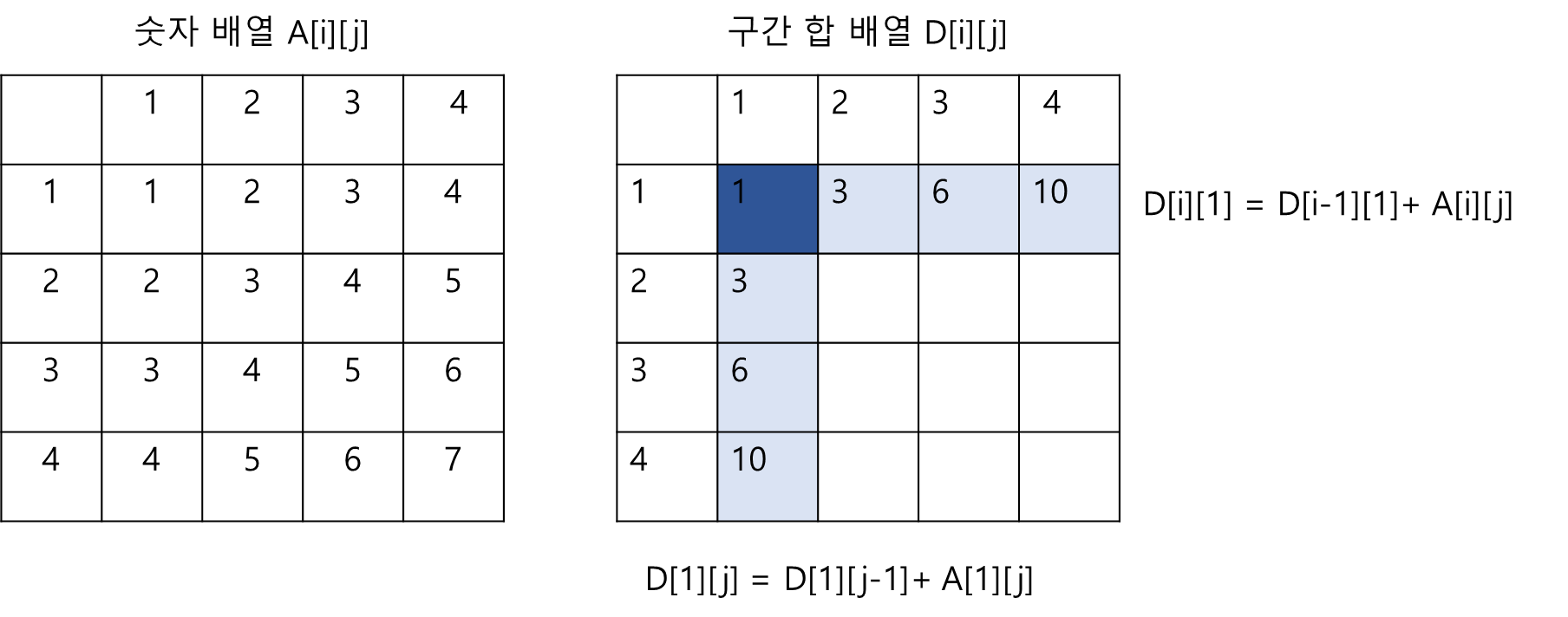
2️⃣ 나머지 2차원 구간 합 배열 채우기
- D[i][j]의 값을 채우는 구간 합 공식
- D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
3️⃣ 답 도출 과정
- 질의 2 2 3 4
- (2,2) 에서 (3,4) 까지의 구간 합
- (1,1) 에서 (3, 4)까지의 구간 합 - (1,1) 에서 (1,4) 까지의 구간합 - (1,1) 에서 (3,1)까지 구간합
- + (1,1) 구간 합
- D[3][4] - D[1][4] - D[3][1] + D[1][1] = 27
- 질의 공식 (x1, y1), (x2, y2)에 대한 구간 합 구하기
- D[x2][y2] - D[x1-1][x2] - D[x2][y1-1] + D[x1-1][y1-1]
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main{
public static void main(String [] agrs) throws IOException{
//입력받기
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// n * n 배열의 n
int N = Integer.parseInt(st.nextToken());
// query num
int M = Integer.parseInt(st.nextToken());
//n * n 배열에 값 담기
int A[][] = new int[N + 1][N + 1];
for(int i = 1; i <= N; i++){
st = new StringTokenizer(br.readLine());
for(int j = 1; j <= N; j++){
A[i][j] = Integer.parseInt(st.nextToken());
}
}
//구간 합을 구해서 구간 합에 담기
int D[][] = new int[N+1][N+1];
for(int i = 1; i <= N; i++){
for(int j = 1; j <= N; j++){
//구간 합 구하는 공식
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j];
}
}
// 질의 수 만큼 구해서 출력하기
for(int i = 0 ; i < M; i++){
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
// 구간 합 배열로 질의 답
int result = D[x2][y2] - D[x2][y1-1] - D[x1-1][y2] + D[x1-1][y1-1];
System.out.println(result);
}
}
}
'Algorithm' 카테고리의 다른 글
| [백준 1018] 체스판 다시 칠하기 (1) | 2024.02.17 |
|---|---|
| 백준 [27866] 문자와 문자열 - Java (1) | 2024.02.14 |
| 백준[10250] ACM 호텔 - Java (0) | 2024.02.14 |
| 백준[11659] - 구간 합 구하기 4 (0) | 2022.12.30 |
| 백준[5585번] :: 거스름돈(Java11, 자바) (1) | 2021.02.02 |
본 포스팅은 “Do it! 알고리즘 코딩 테스트 자바 편” 의 학습용도입니다.

문제분석하기
- 질의의 개수가 10만이므로, 질의마다 합을 구하면 안되고, 구간 합 배열을 이용해야 한다.
- 구간 합 배열이 1차원에서 2차원으로 확장된 것으로 생각하여 구간 합 배열을 어떻게 구성할지 고민하는 것이 이 문제의 핵심이다.
- 2차원 구간 합 배열은 다음과 같이 정의할 수 있다.
2차원 구간 합 배열 D[X][Y]의 정의
- D[X][Y] = 원본 배열의 (0,0) 부터 (X,Y)까지의 사각형 영역 안에 있는 수의 합
- 1차원 배열 구간 합이 궁금하다면?
백준[11659] - 구간 합 구하기 4
✏️ 문제분석 수의 개수와 합을 구해야 하는 횟수는 최대 10만 구간마다 합을 매번 계산하면 0.5초 안에 모든 구간 합계산을 끝낼 수 없음 💡 구간 합을 매번 계산하면 최악의 경우, 1억 회 이상
muscleking3426.tistory.com
손으로 풀어보기
1️⃣ 2차원 구간 합 배열의 1행 1열 부터 구한다. 구간 합 배열의 1행, 1열은 다음과 같이 구할 수 있다.
i : 행 / j : 열

2️⃣ 나머지 2차원 구간 합 배열 채우기
- D[i][j]의 값을 채우는 구간 합 공식
- D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
3️⃣ 답 도출 과정
- 질의 2 2 3 4
- (2,2) 에서 (3,4) 까지의 구간 합
- (1,1) 에서 (3, 4)까지의 구간 합 - (1,1) 에서 (1,4) 까지의 구간합 - (1,1) 에서 (3,1)까지 구간합
- + (1,1) 구간 합
- D[3][4] - D[1][4] - D[3][1] + D[1][1] = 27
- 질의 공식 (x1, y1), (x2, y2)에 대한 구간 합 구하기
- D[x2][y2] - D[x1-1][x2] - D[x2][y1-1] + D[x1-1][y1-1]
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main{
public static void main(String [] agrs) throws IOException{
//입력받기
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// n * n 배열의 n
int N = Integer.parseInt(st.nextToken());
// query num
int M = Integer.parseInt(st.nextToken());
//n * n 배열에 값 담기
int A[][] = new int[N + 1][N + 1];
for(int i = 1; i <= N; i++){
st = new StringTokenizer(br.readLine());
for(int j = 1; j <= N; j++){
A[i][j] = Integer.parseInt(st.nextToken());
}
}
//구간 합을 구해서 구간 합에 담기
int D[][] = new int[N+1][N+1];
for(int i = 1; i <= N; i++){
for(int j = 1; j <= N; j++){
//구간 합 구하는 공식
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j];
}
}
// 질의 수 만큼 구해서 출력하기
for(int i = 0 ; i < M; i++){
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
// 구간 합 배열로 질의 답
int result = D[x2][y2] - D[x2][y1-1] - D[x1-1][y2] + D[x1-1][y1-1];
System.out.println(result);
}
}
}
'Algorithm' 카테고리의 다른 글
| [백준 1018] 체스판 다시 칠하기 (1) | 2024.02.17 |
|---|---|
| 백준 [27866] 문자와 문자열 - Java (1) | 2024.02.14 |
| 백준[10250] ACM 호텔 - Java (0) | 2024.02.14 |
| 백준[11659] - 구간 합 구하기 4 (0) | 2022.12.30 |
| 백준[5585번] :: 거스름돈(Java11, 자바) (1) | 2021.02.02 |
